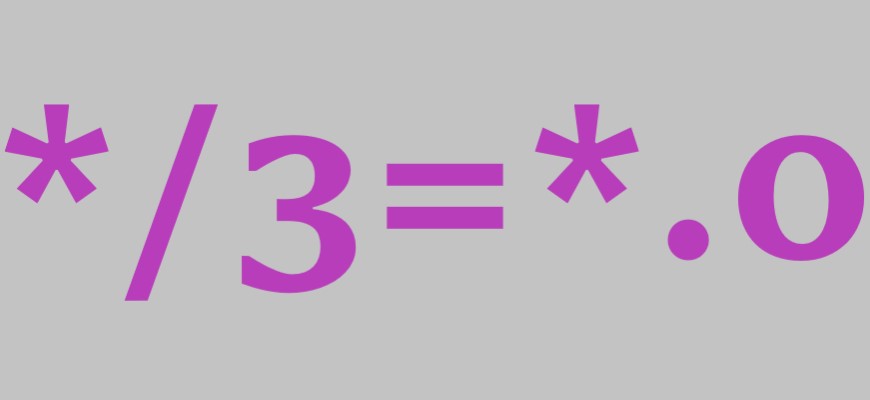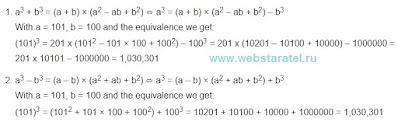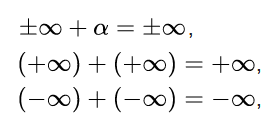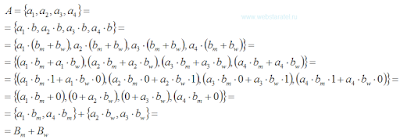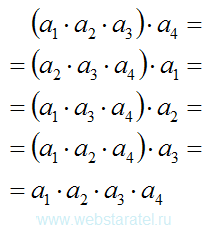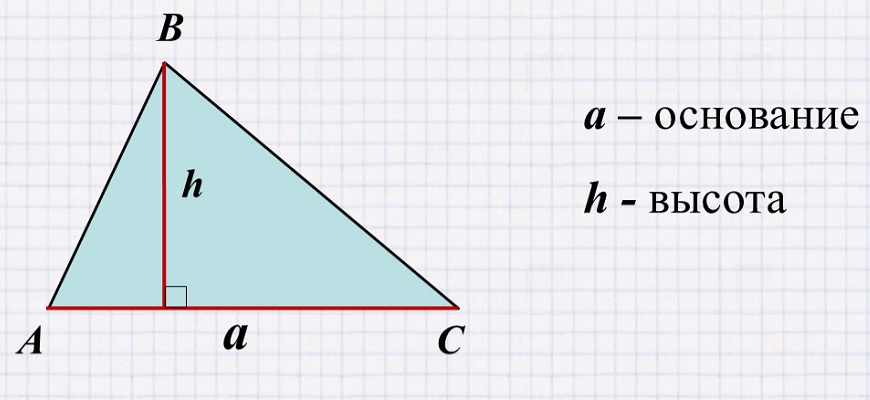
Через основание и высоту Одна из двух «базовых», наиболее часто используемых формул. Именно через нее доказывается большинство прочих. Чтобы узнать площадь
Аннотация Если взять любую сумму, то все остальные суммы можно разделить на три группы: одинаковые суммы, суммы разложения и другие суммы.
Аннотация Применение сдвига в арифметике приводит к сложению слагаемых с разными единицами измерения. Рассмотрим результаты сдвига в арифметическом сложении.
Аннотация При выполнении математических действий с бесконечными рядами необходимо соблюдать правила позиционной системы счисления. Количество слагаемых
Со школьной скамьи всем нам известно правило, появившееся ещё в древности: от перестановки мест слагаемых сумма не меняется. Об этом матемаики никогда
В прошлый раз я рассказывал, как математики обманывают маленьких детей. Сейчас я покажу, как они обманывают взрослых. То, что вы увидите —
Квадратура круга. Решение задачи. Почти точное. Математический розыгрыш. Квадратура круга. Решение задачи. Почти точное. Это построение не является решением
Я не буду здесь рассказывать вам, что такое знак больше и меньше, я расскажу вам, как их запомнить. В далекие-далекие времена, когда я был маленьким и
Сколько будет 2 в ноль пятой степени? Вопрос с подвохом, как и всё то, что придумывают для нас математики. Если кратко, преобразования выглядят вот так.
Как найти 101 в кубе, используя формулы сокращенного умножения? Я уже показывал, как при помощи формулы куба суммы можно вычислить сто один в кубе.
Сегодня мы разберем пример, как при помощи формул сокращенного умножения можно найти сто один в кубе. Другими словами, как число 101 возвести в третью
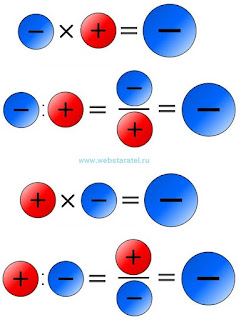
Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных
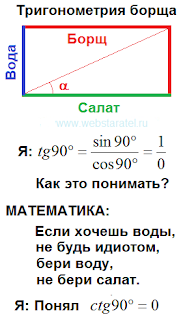
Я не стану вам рассказывать рецепты приготовления борща, я буду говорить о математике. Что такое борщ? Если говорить просто, то это овощи, приготовленные
Просмотрел интересное видио про ряд Гранди. Один минус один плюс один минус один — Numberphile. Математики врут. Они не выполнили проверку равенства
Дописывал постскриптум к статье о загадке вавилонской таблички и увидел в Википедии этот замечательный текст: Вавилонская математика Читаем: «
Завершая разговор о множествах, нужно рассмотреть бесконечное множество. Дало в том, что понятие «бесконечность» действует на математиков, как
Как разделить множество на подмножества? Для этого необходимо ввести новую единицу измерения, присутствующую у части элементов выбранного множества.
Ахиллес и черепаха В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «
Я вам уже рассказывал, что теория множеств — это теория стада, при помощи которой шаманы пытаются сортировать «морских ежей»
Если математики не могут свести понятие «множество» к другим понятиям, значит они ничего не понимают в математике. Отвечаю на вопрос: чем элементы